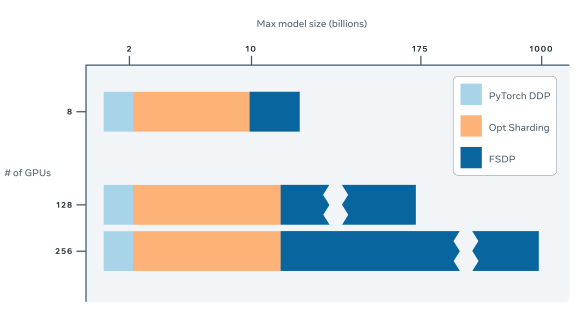
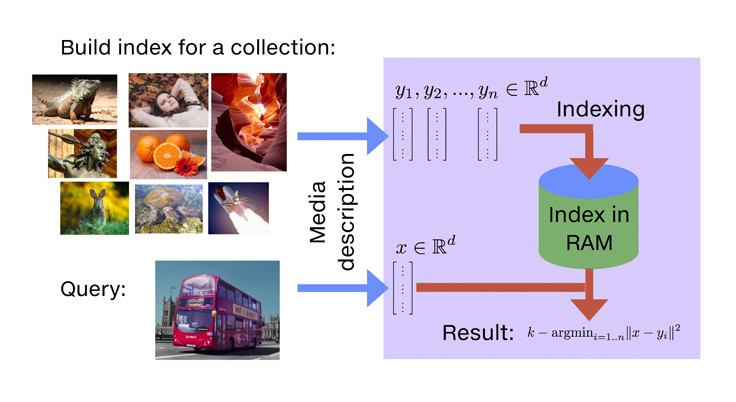
Faiss: A library for efficient similarity search

This month, we released Facebook AI Similarity Search (Faiss), a library that allows us to quickly search for multimedia documents that are similar to each other — a challenge where traditional query search engines fall short. We’ve built nearest-neighbor search implementations for billion-scale data sets that are some 8.5x faster than the previous reported state-of-the-art, along with the fastest k-selection algorithm on the GPU known in the literature. This lets us break some records, including the first k-nearest-neighbor graph constructed on 1 billion high-dimensional vectors.

About similarity search

Traditional databases are made up of structured tables containing symbolic information. For example, an image collection would be represented as a table with one row per indexed photo. Each row contains information such as an image identifier and descriptive text. Rows can be linked to entries from other tables as well, such as an image with people in it being linked to a table of names.

AI tools, like text embedding (word2vec) or convolutional neural net (CNN) descriptors trained with deep learning, generate high-dimensional vectors. These representations are much more powerful and flexible than a fixed symbolic representation, as we’ll explain in this post. Yet traditional databases that can be queried with SQL are not adapted to these new representations. First, the huge inflow of new multimedia items creates billions of vectors. Second, and more importantly, finding similar entries means finding similar high-dimensional vectors, which is inefficient if not impossible with standard query languages.

How can a vector representation be used?

Let’s say you have an image of a building — for example, the city hall of some midsize city whose name you forgot — and you’d like to find all other images of this building in the image collection. A key/value query that is typically used in SQL doesn’t help, because you’ve forgotten the name of the city.

This is where similarity search kicks in. The vector representation for images is designed to produce similar vectors for similar images, where similar vectors are defined as those that are nearby in Euclidean space.

Another application for vector representation is classification. Imagine you need a classifier that determines which images in a collection represent a daisy. Training the classifier is a well-known process: The algorithm takes as input images of daisies and images of non-daisies (cars, sheep, roses, cornflowers). If the classifier is linear, it outputs a classification vector whose property is that its dot product with the image vector reflects how likely it is that the image contains a daisy. Then the dot product can be computed with all entries in the collection and the images with the highest values are returned. This type of query is a “maximum inner-product” search.

So, for similarity search and classification, we need the following operations:

Given a query vector, return the list of database objects that are nearest to this vector in terms of Euclidean distance.
Given a query vector, return the list of database objects that have the highest dot product with this vector.

An added challenge is that we want to do these operations on a large scale, on billions of vectors.

Software packages

The software tools currently available aren’t sufficient for the database search operations described above. Traditional SQL database systems are impractical because they’re optimized for hash-based searches or 1D interval searches. The similarity search functions that are available in packages like OpenCV are severely limited in terms of scalability, as are other similarity search libraries considering “small” data sets (for example, only 1 million vectors). Other packages are research artifacts produced for a published paper to demonstrate performance in specific settings.

With Faiss, we introduce a library that addresses the limitations mentioned above. Among its advantages:

Faiss provides several similarity search methods that span a wide spectrum of usage trade-offs.
Faiss is optimized for memory usage and speed.
Faiss offers a state-of-the-art GPU implementation for the most relevant indexing methods.

Evaluating similarity search

Once the vectors are extracted by learning machinery (from images, videos, text documents, and elsewhere), they’re ready to feed into the similarity search library.

We have a reference brute-force algorithm that computes all the similarities — exactly and exhaustively — and returns the list of most similar elements. This provides the “gold standard” reference result list. Note that implementing the brute-force algorithm efficiently is not obvious, and it often feeds into the performance of other components.

Similarity search can be made orders of magnitude faster if we’re willing to trade some accuracy; that is, deviate a bit from the reference result. For example, it may not matter much if the first and second results of an image similarity search are swapped, since they’re probably both correct results for a given query. Accelerating the search involves some pre-processing of the data set, an operation that we call indexing.

This bring us to the three metrics of interest:

Speed. How long does it take to find the 10 (or some other number) most similar vectors to the query? Hopefully less time than the brute-force algorithm needs; otherwise, what’s the point of indexing?
Memory usage. How much RAM does the method require? More or less than the original vectors? Faiss supports searching only from RAM, as disk databases are orders of magnitude slower. Yes, even with SSDs.
Accuracy. How well does the returned list of results match the brute-force search results? Accuracy can be evaluated by counting the number of queries for which the true nearest neighbor is returned first in the result list (a measure called 1-recall@1), or by measuring the average fraction of 10 nearest neighbors that are returned in the 10 first results (the “10-intersection” measure).

We usually evaluate the trade-off between speed and accuracy for a fixed memory usage. Faiss focuses on methods that compress the original vectors, because they’re the only ones that scale to data sets of billions of vectors: 32 bytes per vector takes up a lot of memory when 1 billion vectors must be indexed.

Many indexing libraries exist for around 1 million vectors, which we call small scale. For example, nmslib contains very efficient algorithms for this. It’s faster than Faiss but requires significantly more storage.

Evaluation on 1 billion vectors

Because the engineering world doesn’t have a well-established benchmark for data sets of this size, we compare against research results.

Precision is evaluated on Deep1B, a collection of 1 billion images. Each image has been processed by a convolutional neural net (CNN), and one of the activation maps of the CNN is kept as an image descriptor. These vectors can be compared with Euclidean distances to quantify how similar the images are.

Deep1B comes with a small collection of query images, and the ground-truth similarity search results are provided from a brute-force algorithm on these images. Therefore, if we run a search algorithm we can evaluate the 1-recall@1 of the result.

Choosing the index

For the sake of evaluation, we limit the memory usage to 30 GB of RAM. This memory constraint guides our choice of an indexing method and parameters. In Faiss, indexing methods are represented as a string; in this case, OPQ20_80,IMI2x14,PQ20.

The string indicates a pre-processing step (OPQ20_80) to apply to the vectors, a selection mechanism (IMI2x14) indicating how the database should be partitioned, and an encoding component (PQ20) indicating that vectors are encoded with a product quantizer (PQ) that generates 20-byte codes. Therefore the memory usage, including overheads, is below 30 GB of RAM.

We know this sounds a bit technical, and that’s why the Faiss documentation provides guidelines on how to choose the index best adapted to your needs.

Once the index type is chosen, indexing can begin. The algorithm processes the 1 billion vectors and puts them into an index. The index can be stored on disk or used immediately, and searches and additions/removals to the index can be interleaved.

Searching in the index

When the index is ready, a set of search-time parameters can be set to adjust the method. For the sake of evaluation, we perform searches in a single thread. Here, we need to optimize the trade-off between accuracy and search time, since memory usage is fixed. This means, for example, being able to set parameters that give a 1-recall@1 of 40 percent in the least possible search time.

Fortunately, Faiss comes with an automatic tuning mechanism that scans the space of parameters and collects the ones that provide the best operating points; that is, the best possible search time given some accuracy, and vice versa. On Deep1B, the operating points can be visualized as a plot:

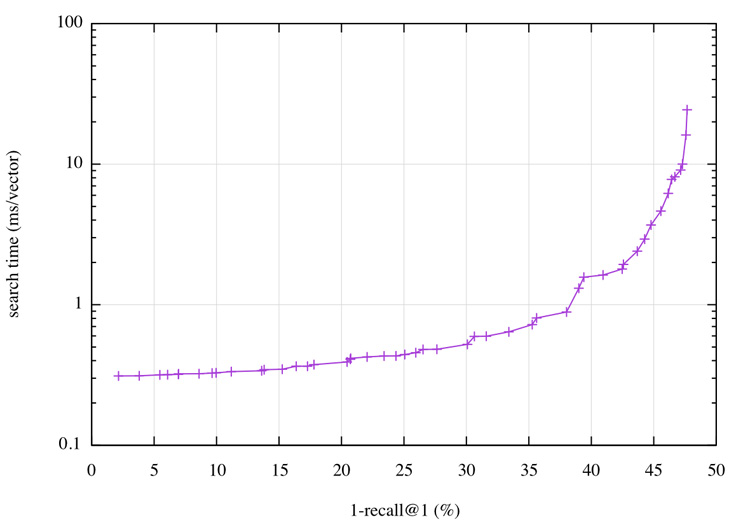
On this plot, we can read that getting a 1-recall@1 of 40 percent has a query time of less than 2 ms per vector, or that with a time budget of 0.5 ms we can reach 30 percent. A 2 ms query time translates to 500 queries per second (QPS) on a single core.

This result can be compared against results from the most advanced research results in the field: “Efficient Indexing of Billion-Scale Datasets of Deep Descriptors” by Babenko and Lempitsky, CVPR 2016, the paper that introduced the Deep1B data set. They need 20 ms to obtain a 1-recall@1 of 45 percent.

Billion-scale data sets with GPUs

A lot of effort went into the GPU implementation, yielding astonishing single-machine performance with native multi-GPU support. The GPU implementations are also drop-in replacements for their CPU equivalents, and you don’t need to know the CUDA API in order to exploit the GPUs. GPU Faiss supports all Nvidia GPUs introduced after 2012 (Kepler, compute capability 3.5+).

We like to use the roofline model as a guide, which states that one should strive to saturate the memory bandwidth or the floating-point units. Faiss GPU is typically 5-10x faster on a single GPU than the corresponding Faiss CPU implementations. New Pascal-class hardware, like the P100, pushes this to 20x+.

Some impressive numbers:

With approximate indexing, a brute-force k-nearest-neighbor graph (k = 10) on 128D CNN descriptors of 95 million images of the YFCC100M data set with 10-intersection of 0.8 can be constructed in 35 minutes on four Maxwell Titan X GPUs, including index construction time.
Billion-vector k-nearest-neighbor graphs are now easily within reach. One can make a brute-force k-NN graph (k = 10) of the Deep1B data set with 10-intersection of 0.65 in under 12 hours on four Maxwell Titan X GPUs, or 0.8 in under 12 hours on eight Pascal P100-PCIe GPUs. Lower-quality graphs can be produced in under 5 hours on the Titan X configuration.
Other components achieve impressive performance. For instance, building the above Deep1B index requires k-means clustering 67.1 million 120-dim vectors to 262,144 centroids, which for 25 E-M iterations takes 139 minutes on the four Titan X GPUs (12.6 tflop/s of compute), or 43.8 minutes on eight P100 GPUs (40 tflop/s of compute). Note that the training set of the clustering does not need to fit in GPU memory, as the data is streamed to the GPU as needed without impact on the performance.

Under the hood

The Facebook AI Research team started developing Faiss in 2015, based on research results and a substantial engineering effort. For this library, we chose to focus on properly optimized versions of a few fundamental techniques. In particular, on the CPU side we make heavy use of:

Multi-threading to exploit multiple cores and perform parallel searches on multiple GPUs.
BLAS libraries for efficient exact distance computations via matrix/matrix multiplication. An efficient brute-force implementation cannot be optimal without using BLAS. BLAS/LAPACK is the only mandatory software dependency of Faiss.
Machine SIMD vectorization and popcount are used to speed up distance computations for isolated vectors.

On the GPU side

For previous GPU implementations of similarity search, k-selection (finding the k-minimum or maximum elements) has been a performance problem, as typical CPU algorithms (heap selection, for example) are not GPU friendly. For Faiss GPU, we designed the fastest small k-selection algorithm (k <= 1024) known in the literature. All intermediate state is kept entirely in registers, contributing to its high speed. It is able to k-select input data in a single pass, operating at up to 55 percent of peak possible performance, as given by peak GPU memory bandwidth. Because its state is retained solely in the register file, it is fusible with other kernels, lending itself to blazing-fast exact and approximate search algorithms.

Much attention was paid to efficient tiling strategies and implementation of kernels used for approximate search. Multi-GPU support is provided by either sharding or replicating data; one is not limited to the memory available on a single GPU. Half-precision floating-point support (float16) is provided as well, with full float16 compute on supporting GPUs and intermediate float16 storage provided on earlier architectures. We found that encoding vectors as float16 yields speedup with almost no loss of accuracy.

In short, constant overhead factors matter in the implementation. Faiss did much of the painful work of paying attention to engineering details.

Try it out

Faiss is implemented in C++ and has bindings in Python. To get started, get Faiss from GitHub, compile it, and import the Faiss module into Python. Faiss is fully integrated with numpy, and all functions take numpy arrays (in float32).

The index object

Faiss (both C++ and Python) provides instances of Index. Each Index subclass implements an indexing structure, to which vectors can be added and searched. For example, IndexFlatL2 is a brute-force index that searches with L2 distances.


import faiss                   # make faiss available
index = faiss.IndexFlatL2(d)   # build the index, d=size of vectors 
# here we assume xb contains a n-by-d numpy matrix of type float32
index.add(xb)                  # add vectors to the index
print index.ntotal

This will display the number of indexed vectors. Adding to an IndexFlat just means copying them to the internal storage of the index, since there is no processing applied to the vectors.

To perform a search:


# xq is a n2-by-d matrix with query vectors
k = 4                          # we want 4 similar vectors
D, I = index.search(xq, k)     # actual search
print I

I is an integer matrix. The output is something like this:


[[  0 393 363  78]
 [  1 555 277 364]
 [  2 304 101  13]]

For the first vector of xq, the index of the most similar vectors in xb is 0 (0-based), the second most similar is #393, the third is #363, and so on. For the second vector of xq, the list of similar vectors is #1, #555, etc. In this case, the first three vectors of xq seem to be the same as the first three of xb.

Matrix D is the matrix of squared distances. It has the same shape as I and indicates for each result vector at the query’s squared Euclidean distance.

Faiss implements a dozen index types that are often compositions of other indices. The optional GPU version has exactly the same interface, and there are bridges to translate between CPU and GPU indices. The Python interface is mostly generated from the C++ to expose the C++ indices, so it’s easy to translate Python validation code to integrated C++.