Facebook’s codebase changes each day as engineers develop new features and optimizations for our apps. If not validated, each of these changes could potentially regress the functionality or reliability of our products for billions of people around the world. To mitigate this risk, we maintain an enormous suite of automated regression tests to cover various products and apps. These tests are run at each stage of the development process, helping engineers detect regressions early and prevent them from affecting our products.
While we use automated tests to detect regressions in product quality, until recently we had no means of automatically detecting whether the tests themselves were deteriorating. Automated tests are another piece of software that can become unreliable over time as the codebase evolves. Unreliable, also known as flaky, tests produce false or nondeterministic signals that undermine engineers’ trust and thus the effectiveness of the entire regression testing process. If a test sometimes passes and sometimes fails, without a change to the underlying product or app, it forces engineers to spend their time chasing down issues that may not even exist. This undermines their trust in the testing process. It is thus important to determine whether a test has become flaky.
To date, academic research has focused primarily on trying to identify which tests are flaky and which are reliable. Software engineering practice, however, shows that all real-world tests are flaky to some extent, even if they are implemented following best engineering principles. Thus, the right question to ask is not whether a particular test is flaky, but how flaky it is. To answer this question, we’ve developed a measure of test flakiness: the probabilistic flakiness score (PFS). Using this measure, we can now test the tests to measure and monitor their reliability, and thus be able to react quickly to any regressions in the quality of our test suite.
PFS allows us to quantify the degree of flakiness for each individual test at Facebook and to monitor changes in its reliability over time. If we detect specific tests that became unreliable soon after they were created, we can direct engineers’ attention to repairing them. The score is universal, meaning it is applicable to every regression test, irrespective of the programming language or test framework in use. Additionally, it can be efficiently calculated, which lets us scale it to monitor reliability of millions of tests in real time. This measure of test flakiness is interpretable and understandable by an average engineer. For this reason, PFS has been adopted by many Facebook teams to set test reliability goals and drive cross-team efforts to repair flaky tests.
Why PFS?
When a test is flaky, engineers quickly learn to ignore it and eventually remove it, which increases the risk of future code changes regressing functionality or quality. A few years ago, we created a way to use machine learning to predict which tests to run on a particular code change. At the time, we realized that small, targeted tests might be somewhat flaky, but that’s tolerable and easily resolved by retrying or modifying the test.
When we get to bigger end-to-end tests, however, reliability is a bigger challenge. Retrying those multiple times is time-consuming, and trying to modify the test is far more complex. We need a very reliable signal when code changes are made, so developers won’t waste time chasing down problems that don’t really exist. At the time, we assumed that a truly reliable test would never show a regression where there wasn’t one. To know which tests were truly reliable, we needed an automated way to test the tests.
We set out to find tests that don’t show any unreliable behavior (sometimes passing, sometimes not). We quickly realized that there aren’t any — all end-to-end tests have some degree of flakiness. There’s always something that could go wrong that would affect the reliability of the tests. A test that was reliable yesterday might be flaky today, depending on a variety of factors. Which means that we also need to monitor the reliability of our tests on an ongoing basis, to be alerted when a test’s flakiness increases beyond what’s tolerable.
Ultimately, our goal with PFS is not to assert that any test is 100 percent reliable, because that’s not realistic. Our goal is to simply assert that a test is sufficiently reliable and provide a scale to illustrate which tests are less reliable than they should be.
How does PFS work?
30,000-foot view
In the absence of any additional information, we must take the result of a single test execution at face value — we have no basis to tell whether this result is a symptom of test flakiness or a legitimate indicator that the test has detected a regression. However, if we execute a particular test multiple times and it manifests a constant degree of flakiness, we can reasonably expect to observe concrete distribution of results.
In order to measure flakiness of any test, we have developed a statistical model that produces a distribution of results similar to one that would be observed had a test manifesting a known flakiness been exercised a number of times. We have implemented the model in a probabilistic programming language, Stan.
The model lets us generate a distribution of test results provided we set the desired level of flakiness of a hypothetical test. However, when using the model, we know recent test results of a concrete, real-world test and want to estimate flakiness this test exhibits. A procedure that allows us to invert the model is called Bayesian inference. It is implemented very efficiently by the probabilistic programming language runtime and thus we don’t need to worry about it much.
What affects the result of a test
To better understand our statistical (quantitative) model we will consider a simpler, qualitative one first. The simplified model isolates three large factors that affect test results:
- Whether a test fails definitely depends on the code under test and the code defining the test itself. Dependency of a test’s outcome on the version of the code is desirable. It’s entirely possible for a test to have invalid assertions, although such tests are typically identified and fixed or removed quickly.
- Many comprehensive, more end-to-end tests also rely on services deployed in production to function correctly. Some of them even check compatibility of the code under test with those services. Just as behavior of the code under test depends on feature gating and all sorts of configurations, so does the outcome of a test that exercises this code. Therefore, the dependency of a test’s result on the state of the world is frequently inevitable and occasionally desirable.
- Lastly, we have a rubbish bin. Anything else that affects test outcome falls into this category. In particular, there are many nondeterministic factors affecting test executions, such as race conditions, use of randomness, or spurious failures when talking over a network. We call this rubbish-bin flakiness, and this is precisely what we want to measure and understand.
In the above qualitative model, the degree of sensitivity of the test result with respect to the last factor constitutes our measure of flakiness. Conceptually, had the result of a test been differentiable, we could have written down our flakiness score as follows.

Unfortunately, the result of the test is binary, and we cannot calculate the above partial derivative. We must find another way to quantify how sensitive the result of a particular test is with respect to the flakiness factor.
Asymmetry of test results
In our early attempts at constructing the statistical model, we stumbled upon an interesting problem: The underlying mathematics were symmetrical with respect to replacing passing and failing test results. Drawing from our own software engineering experience, we know this is now reflective of how developers perceive test flakiness. We have made the following empirical observation:
A passing test indicates the absence of corresponding regression, while a failure is merely a hint to run the test again.
This asymmetry in how passing and failing test results are treated is an idiosyncrasy of software development. While engineers tend to trust passing test results, they often retry failing tests a number of times on the same version of code and consider failures followed by passing results as flaky. We do not have a good theoretical explanation for why this behavior prevails.
Combining the above observations lets us write our statistical measure of test flakiness, the Probabilistic Flakiness Score, as follows.

Intuitively, the score measures how likely the test is to fail, provided it could have passed on the same version of code and in the same state of the world, had it been retried an arbitrary number of times. Per our empirical observation, if a test can pass after an arbitrary number of retries, any observed failure on the same version of code and state of the world must be considered flaky.
In the above formula, we use conditional probability, which captures the notion of a probability of a particular event occurring (the test failing) provided a particular condition is satisfied (any observed failure is flaky).
The statistical model
To devise our statistical model, we assume that PFS is an intrinsic property of each test — in other words, that each test has a number like that baked into it and our goal is to estimate it based on the observed sequence of test results. In our model, each test is parameterized by not one but two such numbers:
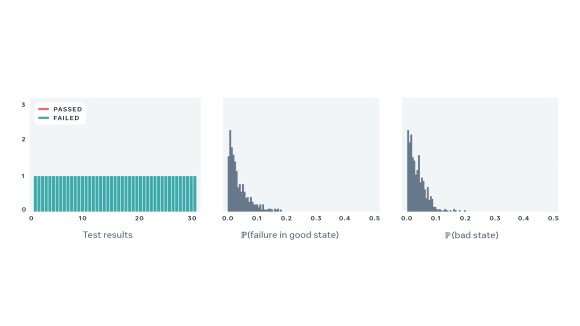
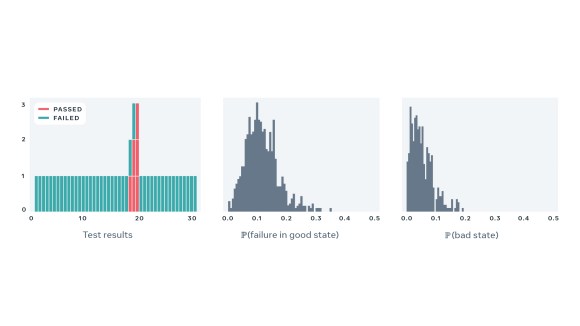
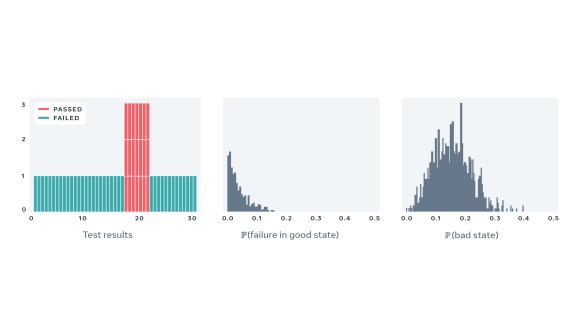
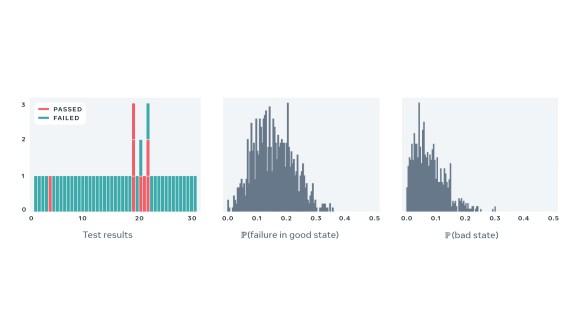
- Probability of bad state, which measures how often the test fails due to the version of the code under test or the state of the world.
- Probability of failure in a good state, which equals the PFS.
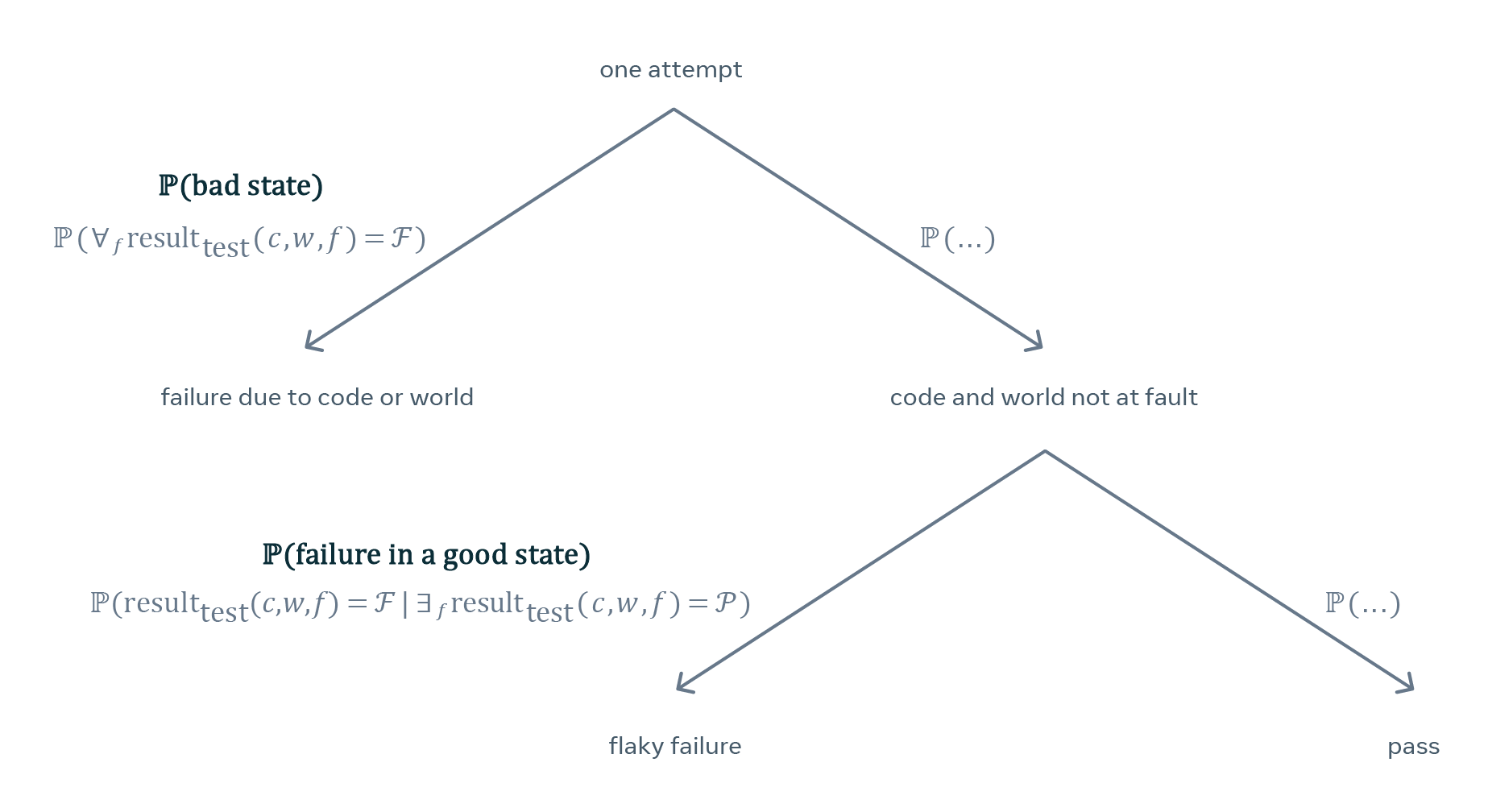
The model does not let us predict future results of a particular test or tell whether a particular failure was caused by the version of code, state of the world, or flakiness. It does, however, let us assess how likely a test characterized by a particular level of flakiness would produce a given sequence of test results.
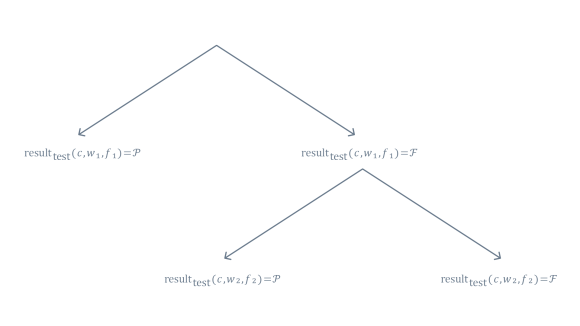
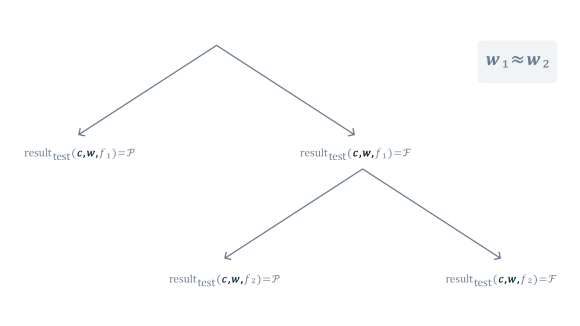
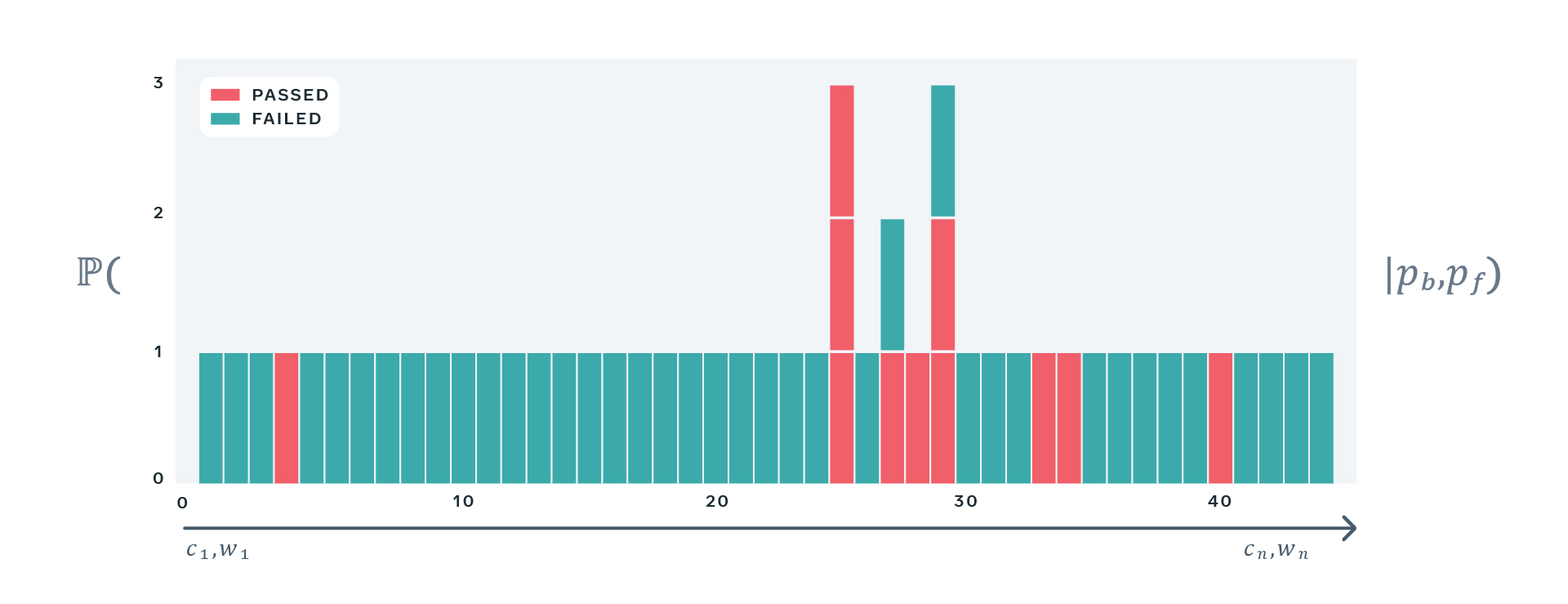
We can see the model in action on a very simple example. Consider a particular test that has been run on a version of the code c and under state of the world w1. If the first attempt passes, we’re done, as per observed asymmetry of test results; we do not retry passing test executions. If the first attempt has failed, however, we do retry a test once. We treat the second attempt as the final outcome of the test, irrespective of whether it passed or failed — we cannot keep retrying the test indefinitely, and in this example we set a limit of one retry for simplicity.
Note that when we retry the test, it is necessarily exercised on the same version of the code, however it may observe a different state of the world. However, because both attempts happened very close to each other in time, it is extremely unlikely that they have observed different states of the world. In fact, our testing infrastructure makes conscious effort to ensure that all retries of a particular test observe a very similar state of the world. For example, we pin all attempts to the same version of configuration or external services. For this reason, in our model we assume that the observed state of the world does not change between attempts.
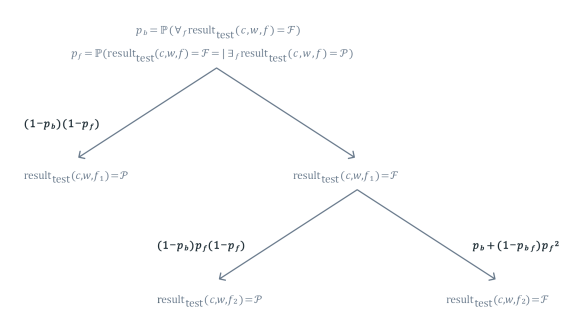
Having all pieces of the puzzle together, we can work out how likely we are going to observe possible test results in terms of the two parameters of the test:
- pb — the probability of bad state
- pf — the probability of failure in good state
Measuring flakiness
The model lets us assess the probability of observing a particular sequence of test results provided the test in question has specific values of the two parameters. However, the values of these parameters are not known a priori. We need to somehow invert the model, in order to estimate them based on the observed sequence of test results.

What comes to the rescue is the Bayes theorem.
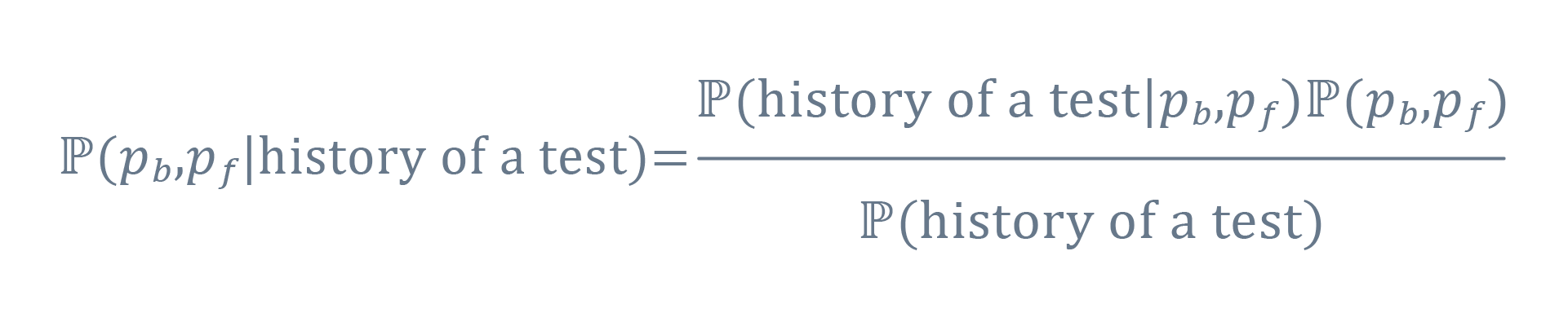
We have expressed the model in statistical modeling environment Stan, which implements state-of-the-art Bayesian inference algorithms. This allows us to efficiently turn a sequence of recently observed test results for a particular test into distribution of the two parameters.
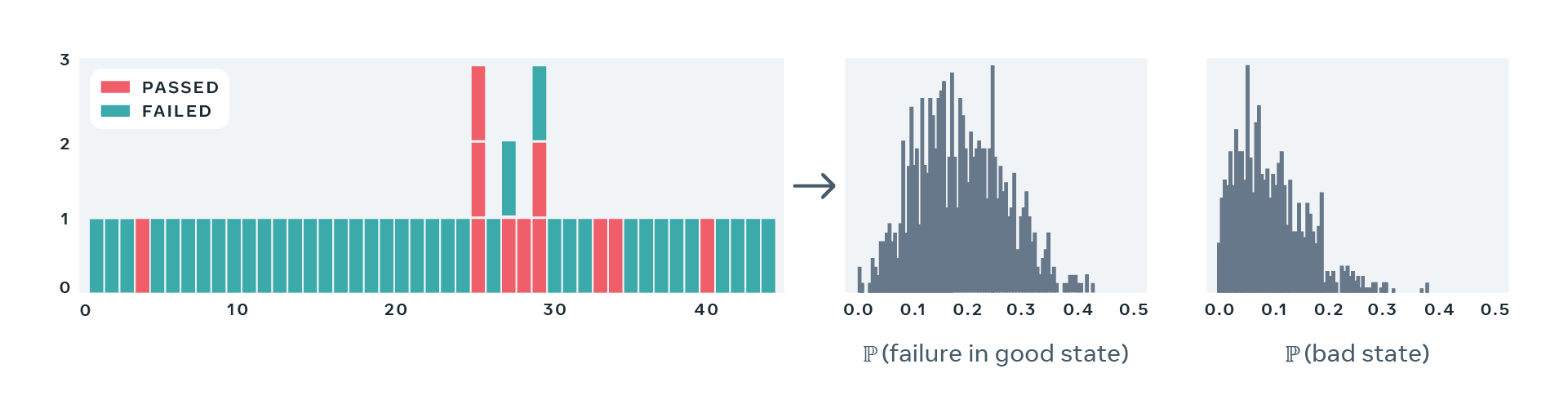
Note that instead of producing point estimates of the PFS, our model yields an entire posterior distribution. This lets us quantify how confident we are in our estimate of the flakiness score:
- When the distribution is narrow and concentrated around a particular flakiness score, we can trust the estimate, as it’s extremely unlikely that the true degree of flakiness is significantly different from our estimate.
- When the distribution is wide or has multiple distinct local maxima, it’s a sign that our model cannot confidently estimate flakiness of a particular test and thus we must take more test results into account to assess how flaky the test is.
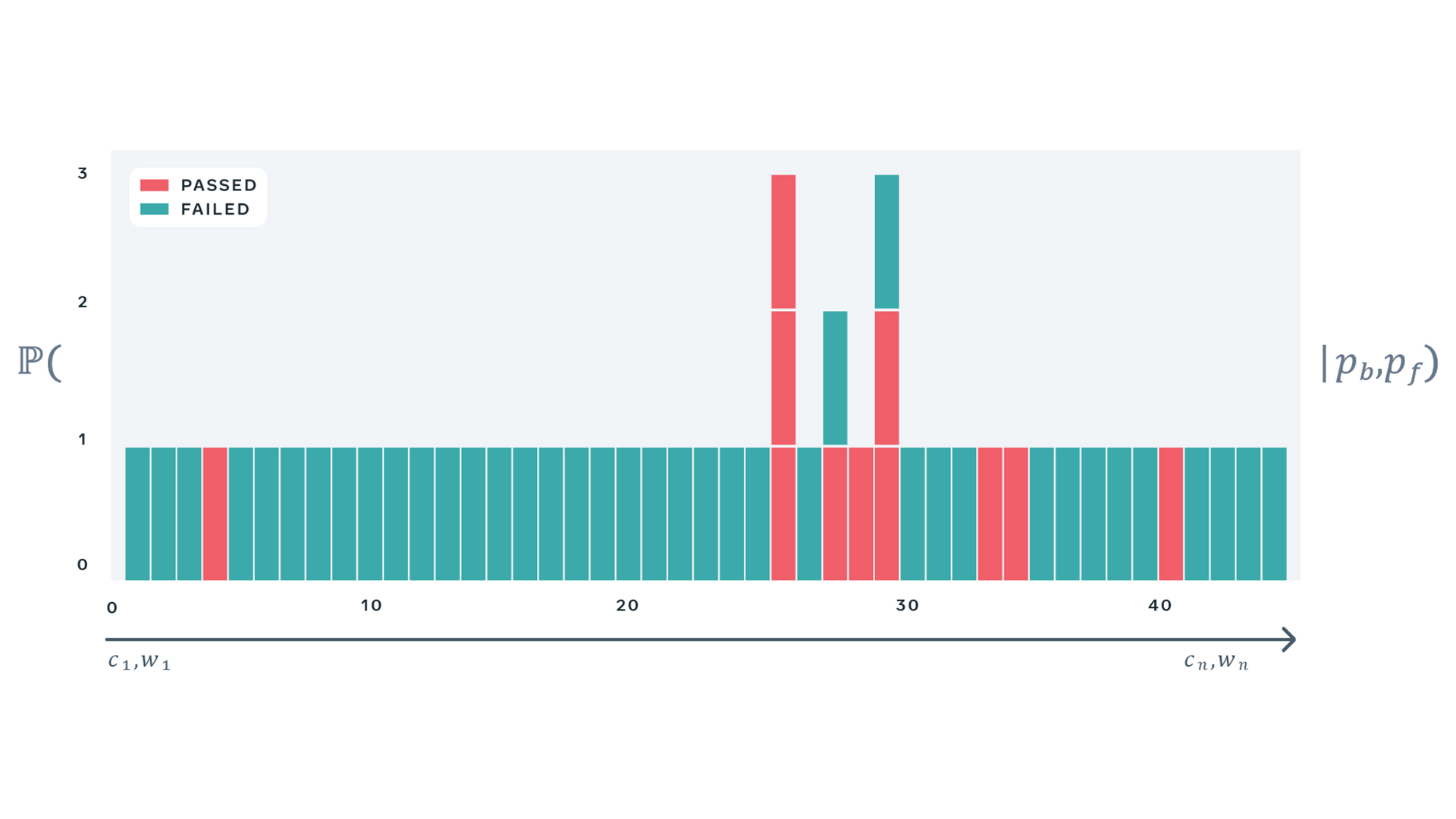
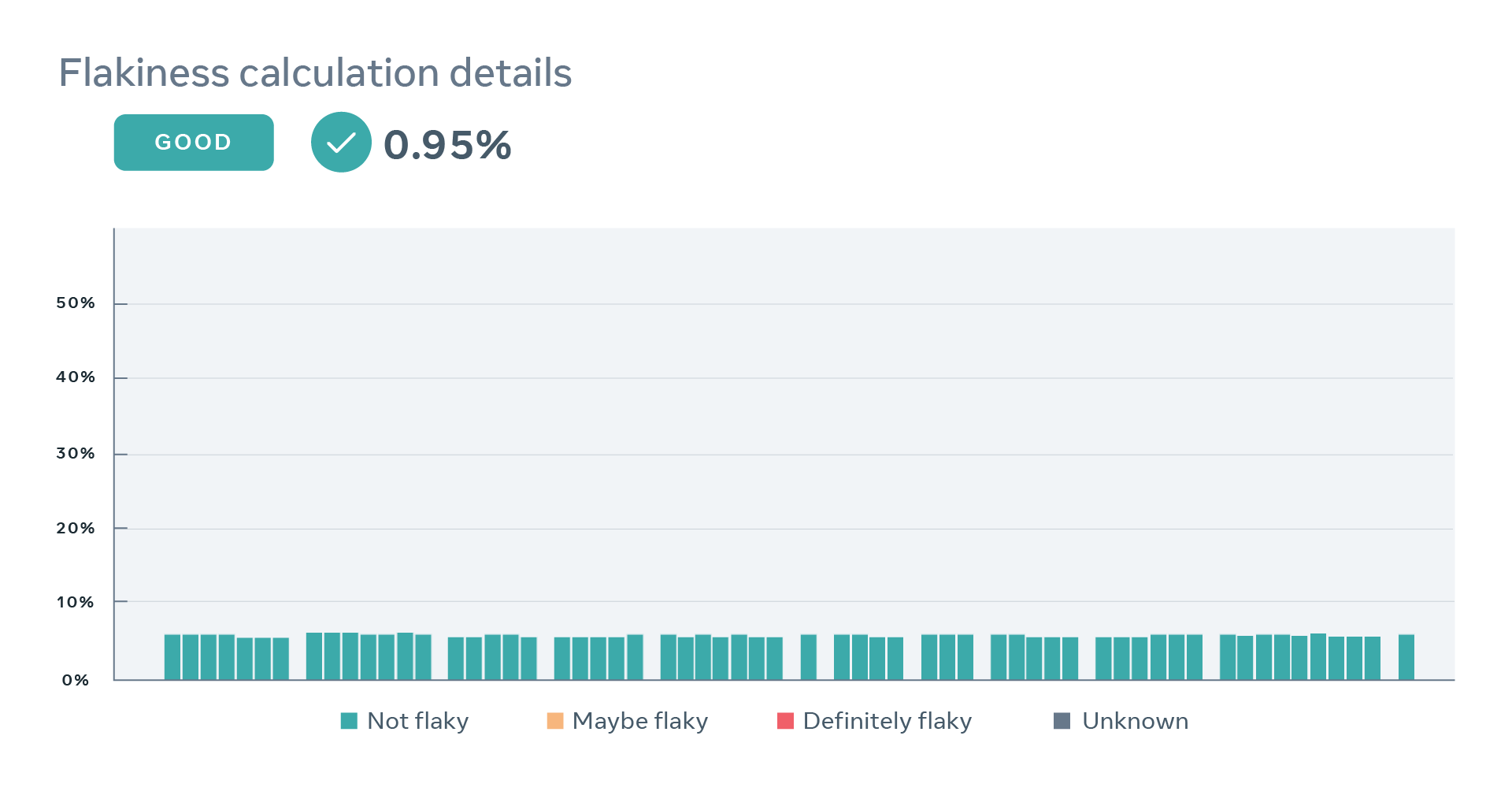
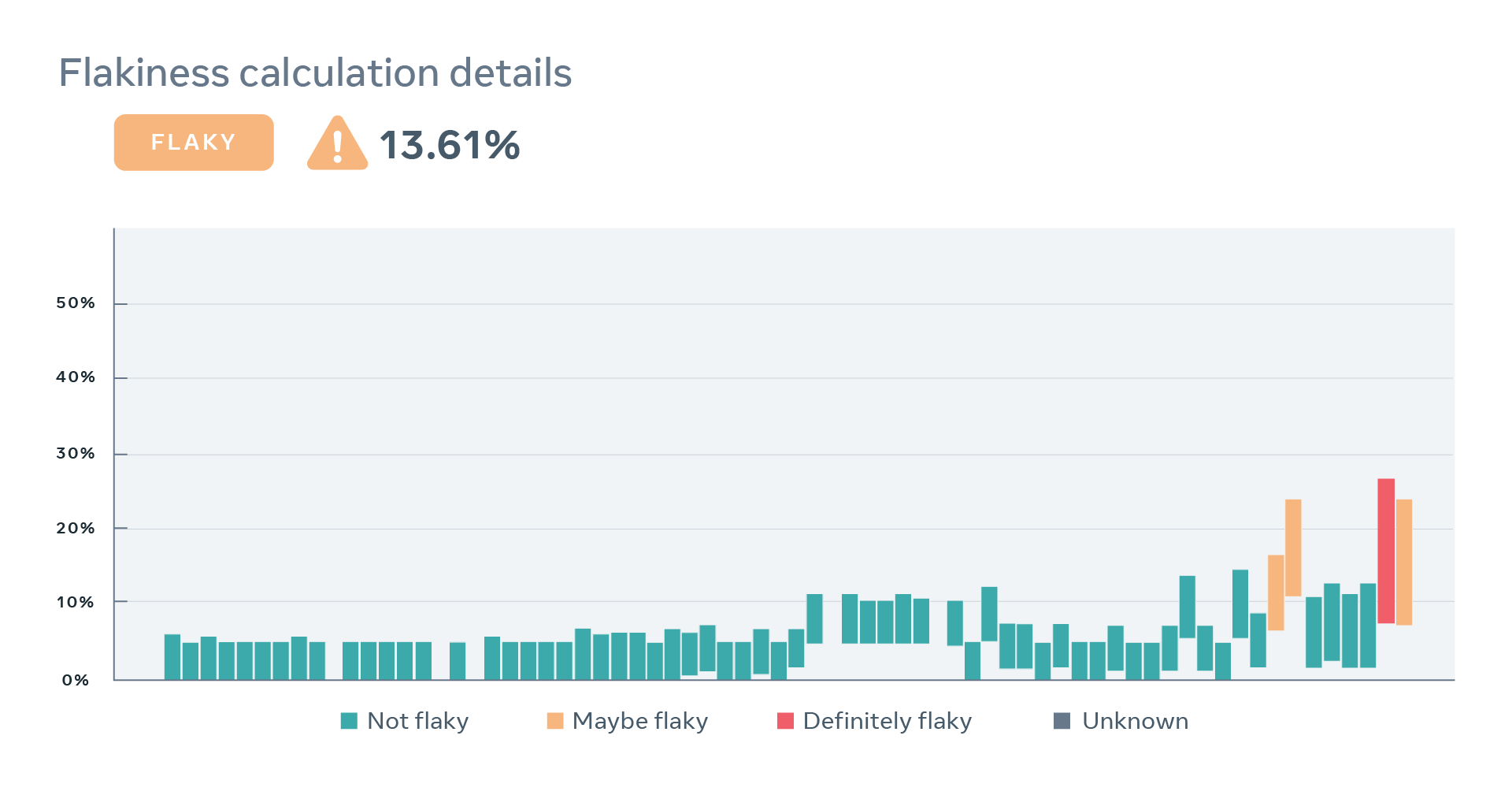
Below, we present four examples of real-world tests, together with a sequence of recent results and estimated values of the two parameters describing behavior of each test. These examples demonstrate flakiness as measured by our statistical model matches what developers would expect eyeballing a sequence of recent results of a particular test. Note that the model correctly captures the case where a perfectly deterministic test breaks — for example, due to a change in global configuration for a period of time — in such case, PFS of the test is close to zero, despite many observed failures.
How are we using PFS?
PFS gives us a measure of test flakiness that is:
- universal, in the sense that it applies to any test,
- based only on an observed sequence of results, meaning it works without any customizations and for tests implemented in any programming language or test framework, and
- indicative of how confident one can be in the estimated degree of flakiness of a particular test.
Since the initial deployment in mid-2018, PFS has served multiple purposes.
Carrot and a stick
PFS is our second most powerful weapon against unreliable tests’ negatively affecting developer experience, trailing behind only the resource-intensive retries.
Based on test results produced during normal operation of the continuous integration system, we calculate and maintain up-to-date score values for all tests, on an ongoing basis. Note that, in order to calculate PFS using our statistical model, we do not require additional test runs. Instead, we can piggyback on those already happening under normal circumstances when developers commit changes to the codebase and have them tested by the continuous integration system. Calculating the score by fitting the statistical model to a history of results of a particular test takes a fraction of a second, and thus can be done for each test and each time a new result is produced.
We present historical values of the PFS on a test-specific dashboard so that developers can locate when changes to the score happened and more easily identify their root-causes.
We rely not only on the goodwill of test authors but also on an incentive structure, in order to keep our vast test suite reliable. When a particular test’s flakiness regresses and starts trending higher, we create a ticket for the declared owner of the test, whether it’s a person or a team. Tests that deteriorate significantly and/or are not fixed on time are marked as flaky, which renders them ineligible for change-based testing. As a result, our continuous integration system will not select such tests to run on changes that potentially affect them. This typically is a strong-enough incentive for test authors to improve a particular test’s reliability, as they heavily rely on tests to enforce contracts with other developers changing our monolithic codebase.
In this way, we use PFS as a carrot and a stick, both encouraging test authors to keep their tests reliable and penalizing those that have let their tests deteriorate to the point that they would have a negative impact on the productivity of other engineers working in the same codebase. PFS helps us resolve natural tension and establish a social contract between test authors and developers changing the codebase. While the former are forced to keep their tests reasonably reliable, the latter must address any issues that reliable tests identify in their code changes.
Metric is trust
Over time, as PFS gained credibility and became more broadly accepted as a measure that reflects developers’ perception of test flakiness, we saw large teams use it to set goals and drive test reliability improvement efforts. This is the best testimony to the level of trust engineers put in PFS doing its job well.
PFS was developed based on the assumption that all tests are flaky to some degree. This is important for a number of reasons when it is used to drive organization-wide investment in test quality. The score helps identify most flaky tests and thus allocate developers’ time toward those tests that, when improved, would most drive down the total level of observed flakiness. While it does not necessarily tell how much work improving a test would require, it does tell you the expected reward.
PFS also helps determine when test quality improvement efforts should stop. Since all tests are flaky, throwing human resources at improving test reliability eventually hits diminishing returns. Every test framework and test environment brings an inherent level of flakiness that cannot be reduced by improving the test. PFS lets us compare the flakiness of a real-world test expressed in a particular test framework with the flakiness of the simplest possible test implemented using the same framework. When these two scores converge, it’s a sign that one cannot make the test any more reliable — unless one decides to improve the framework itself. We’ve observed that this effective flakiness lower-bound varies depending on the test framework in question. For unit tests, it is well below 1 percent, while for some end-to-end test frameworks it reaches 10 percent.
The observation about a portion of test flakiness being contributed by the test framework itself has since found another confirmation. A more recent project in the space of test flakiness led to development of a new, internal end-to-end test framework, which makes it extremely difficult to write unreliable tests and contributes nearly no flakiness by itself.
We’d like to thank the following engineers and acknowledge their contributions to the project: Vladimir Bychkovsky, Beliz Gokkaya, and Michael Samoylenko.